INTEGRABLE MODELS - Research:

• 

  Integrability in Gauge Theory

  One of most exciting recent developments related to the concept of integrability has been the discovery of 3D and 4D interacting quantum field theories which can be studied non-perturbatively using integrable models techniques. The 4D gauge theory, is N = 4 Super Yang-Mills theory, the maximally supersymmetric version of the non-abelian gauge theories which form the backbone of the Standard Model of particle physics; it is superconformal invariant at the quantum level, and it is related to superstring theory on the manifold AdS₅ × S⁵ via the AdS/CFT correspondence. N = 4 Super Yang-Mills (SYM) theory is now at the cross-roads of different lines of research, which attempt to develop a complete understanding of the spectrum and correlation functions of the theory for all values of the coupling, at least in the planar limit.
  
  

• 

  Statistical Models and 2D Quantum Field Theory

  The study of the quantum version of integrable models is based on two initially distinct lines of development. One comes through classical 2D statistical mechanics and quantum 1D spin chains, since any lattice model can be viewed as a regularised Euclidean quantum field theory; the other is the direct study of the models as quantum field theories. On the statistical-mechanical side, the subject can be traced back to Onsager's solution of the simplest integrable lattice model, the two-dimensional Ising model. Viewed directly as a problem in quantum field theory, the history begins with the work in the 1970's on the quantum sine-Gordon model, probably the most famous example of an integrable quantum field theory.
  
  

• 

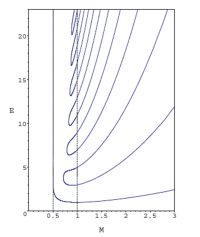
  ODE/IM Correspondence and PT-Symmetric QM

  The study of the 1D Schroedinger equation with polynomial potentials had led, to the discovery that the spectral determinants and Stokes multipliers associated with these problems satisfy exact functional equations. These had enabled exact quantization conditions to be formulated for these problems, but what had not been realised until the year 1998 was that, for certain special potentials, these functional equations, and their solutions, were in fact the same as those arising in the study of thermodynamic Bethe Ansatz for the quantum KdV and the conformal limit of the sine-Gordon model. A link between ordinary differential equations and quantum integrable models is interesting both from the mathematical and the physical points of view, and it has been successfully applied to the study of interacting Bose liquids, quantum dots and other condensed-matter physics models. The generalisation to massive quantum field theories of this correspondence was recently obtained following another, completely different, chain of developments: supersymmetric gauge theories, strings and the correspondence AdS/CFT linking gravity to conformal gauge theory.
  
  

• 

  OAM Beams

  It has been known for a century that electromagnetic beams can carry angular momentum, but only in 1992 it was found theoretically by L. Allen and his collaborators that some types of light beams possess an Orbital Angular Momentum (OAM) of per photon, where is the so-called azimuthal index of the beam. After that a lot of research has been done in order to implement experimental techniques for the creation and the detection of photons in pure OAM states. Nowadays among the several applications of the OAM light beams the most promising are in optical communications, nanotechnologies, quantum optics, biology and astronomy.