



Next: Steepening of the energy
Up: Effects of friction in
Previous: Effects of friction in
Contents
Origin of the friction term
A linear friction term naturally arises in a wide
range of different physical situations, and its origin should
be considered within each specific context.
Here we will briefly consider the case of thin stratified
layers of fluids electromagnetically forced [31,32],
in which the origin of the friction term can be easily understood
starting from the classical three-dimensional Navier-Stokes equations.
The dynamics of a shallow layer of incompressible fluid,
with a thickness 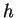 much smaller than its extension
much smaller than its extension 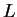 is described by Navier-Stokes equations:
is described by Navier-Stokes equations:
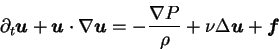 |
(2.1) |
where 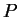 is the pressure,
is the pressure, 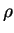 is the density of the fluid,
is the density of the fluid,
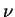 is its kinematic viscosity, and
is its kinematic viscosity, and
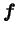 the external forcing.
the external forcing.
In the passage from a three-dimensional to a
two-dimensional description the vertical
components of velocity 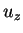 are neglected, since their magnitude with
respect to the horizontal ones
are neglected, since their magnitude with
respect to the horizontal ones 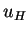 is assumed to be of the
same order of the aspect ratio:
is assumed to be of the
same order of the aspect ratio:
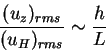 |
(2.2) |
Then we need to parameterize the vertical dependence
of horizontal velocities.
Experimental results [31] suggest that the flow structure
within the layer is close to a Poiseuille flow, so
we can assume a laminar viscous profile of velocities in the 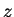 -direction:
-direction:
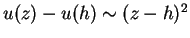 . With this assumption the
three dimensional viscous term in eq.(2.1)
gives origin to a two dimensional viscous term plus
an additional linear damping term, which represent the effects
of the bottom friction of the fluid:
. With this assumption the
three dimensional viscous term in eq.(2.1)
gives origin to a two dimensional viscous term plus
an additional linear damping term, which represent the effects
of the bottom friction of the fluid:
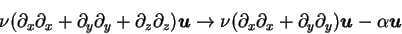 |
(2.3) |
The resulting friction coefficient 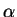 is proportional
to the inverse of the square of the total thickness of the layer
is proportional
to the inverse of the square of the total thickness of the layer 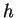 :
:
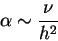 |
(2.4) |
according to the intuitive idea that the thinner is the layer,
the stronger it feels the bottom friction.




Next: Steepening of the energy
Up: Effects of friction in
Previous: Effects of friction in
Contents
Stefano Musacchio
2004-01-09
![]() much smaller than its extension
much smaller than its extension ![]() is described by Navier-Stokes equations:
is described by Navier-Stokes equations:
![]() are neglected, since their magnitude with
respect to the horizontal ones
are neglected, since their magnitude with
respect to the horizontal ones ![]() is assumed to be of the
same order of the aspect ratio:
is assumed to be of the
same order of the aspect ratio: