



Next: Fene-p
Up: Oldroyd-B model
Previous: Newtonian limit: viscosity renormalization
Contents
The free energy of the viscoelastic fluid
is the sum of kinetic and elastic contributions:
![\begin{displaymath}
\mathcal{F} = \int d^3 r \left\{ {1\over 2} \rho u^2 +
{\et...
...sigma$}} - \log \det {\mbox{\boldmath$\sigma$}} ] \right\} \;.
\end{displaymath}](img546.png) |
(3.30) |
where the last term represents the entropy of polymer molecules.
The rate of change of the different components of the free energy
can be obtained from Eqs. (3.24,3.20)
![\begin{displaymath}
{\partial \over \partial t} {1\over 2} u^2 =
{\mbox{\boldma...
...{\boldmath$u$}_i + \sigma_{ij} \nabla_i \mbox{\boldmath$u$}_j]
\end{displaymath}](img547.png) |
(3.31) |
![\begin{displaymath}
{\partial \over \partial t} \textrm{tr}{\mbox{\boldmath$\sig...
...extrm{tr} [{\mbox{\boldmath$\sigma$}} - {\mbox{\boldmath$1$}}]
\end{displaymath}](img548.png) |
(3.32) |
![\begin{displaymath}
{\partial \over \partial t} \log \det {\mbox{\boldmath$\sigm...
...r}[{\mbox{\boldmath$\sigma$}}^{-1} - {\mbox{\boldmath$1$}}]\;.
\end{displaymath}](img549.png) |
(3.33) |
The forcing provides the input of kinetic energy which is
then partially dissipated due to viscosity and
relaxation of polymers. The term
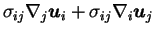 has not a definite sign, and represents
the exchange between kinetic and elastic energy which can goes
in both direction.
Summing together the different contributions one obtain
the rate of change of the free energy:
has not a definite sign, and represents
the exchange between kinetic and elastic energy which can goes
in both direction.
Summing together the different contributions one obtain
the rate of change of the free energy:
![\begin{displaymath}
{\partial \mathcal{F} \over \partial t} =
\rho \int d^3r
\...
...\boldmath$1$}} + {\mbox{\boldmath$\sigma$}}^{-1}]
\right\} \;.
\end{displaymath}](img551.png) |
(3.34) |
Since the conformation tensor
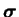 is positive definite
and symmetric, it can always be decomposed as
the product of two symmetric matrices
is positive definite
and symmetric, it can always be decomposed as
the product of two symmetric matrices
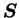 :
:
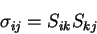 |
(3.35) |
so that the last term, which represent
the energy dissipation rate due to polymers,
can be rewritten as:
![\begin{displaymath}
\textrm{tr}
[{\mbox{\boldmath$\sigma$}} - 2 {\mbox{\boldmath...
...r}
[ ({\mbox{\boldmath$S$}} - {\mbox{\boldmath$S$}}^{-1})^2 ]
\end{displaymath}](img554.png) |
(3.36) |
showing that it has a definite sign.
In the statistically steady state
the average values of the free energy 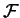 is constant and the energy balance reads:
is constant and the energy balance reads:
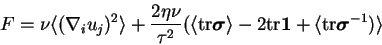 |
(3.37) |
where 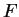 is the average energy input per unit mass.
Assuming that the average kinetic energy and polymer elongation
have statistically constant values, it follows that the
average entropy production rate vanishes
is the average energy input per unit mass.
Assuming that the average kinetic energy and polymer elongation
have statistically constant values, it follows that the
average entropy production rate vanishes
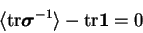 |
(3.38) |
and the entropy of polymer molecule is conserved.




Next: Fene-p
Up: Oldroyd-B model
Previous: Newtonian limit: viscosity renormalization
Contents
Stefano Musacchio
2004-01-09
![\begin{displaymath}
\mathcal{F} = \int d^3 r \left\{ {1\over 2} \rho u^2 +
{\et...
...sigma$}} - \log \det {\mbox{\boldmath$\sigma$}} ] \right\} \;.
\end{displaymath}](img546.png)
![]() is constant and the energy balance reads:
is constant and the energy balance reads: