



Next: Inverse energy cascade
Up: Active polymers
Previous: Lagrangian chaos reduction
Contents
Decaying turbulence
The organization into coherent vortices, starting from
from a disordered background is a characteristic feature of
decaying two-dimensional turbulence (see Chapter 1).
This complex and interesting phenomenology is suppressed by the
presence of a strong friction which halts the flux of energy toward large scales.
Since in this case the energy is mainly dissipated by the linear friction,
the decay of total energy trivially display an exponential behavior
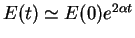 where
where 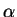 is the friction coefficient.
(see Fig. 4.10).
is the friction coefficient.
(see Fig. 4.10).
Figure:
Decay of mean velocity fluctuation
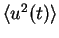 . While in the Newtonian case (dashed line )
the decay is exponential with a rate fixed by the
friction coefficient
. While in the Newtonian case (dashed line )
the decay is exponential with a rate fixed by the
friction coefficient
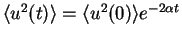 the viscoelastic solution shows an oscillatory behavior with an
exponential trend fixed by the polymer relaxation time.
The oscillations are anti-correlated with those of the mean
elastic energy (see inset). At late stage there is a sharp
decoupling of the polymer and velocity fields which recovers
the Newtonian behavior.
the viscoelastic solution shows an oscillatory behavior with an
exponential trend fixed by the polymer relaxation time.
The oscillations are anti-correlated with those of the mean
elastic energy (see inset). At late stage there is a sharp
decoupling of the polymer and velocity fields which recovers
the Newtonian behavior.
|
|
The coupling with polymer dynamics changes in a different way the decay
of two-dimensional turbulence. Starting from different
configuration randomly chosen from the statistically steady state
above the coil-stretch transition 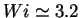 we turned
off the forcing on the velocity field and let the coupled system decay.
In the first stage the balance is dominated by polymer contribution.
An oscillatory decay of the kinetic energy is observable
(see Fig. 4.10), with an exponential trend
fixed by the polymer relaxation time, while the friction term in
the energy balance seems to be sub-dominant. Thus the mean square elongation
of polymers decay exponentially as
we turned
off the forcing on the velocity field and let the coupled system decay.
In the first stage the balance is dominated by polymer contribution.
An oscillatory decay of the kinetic energy is observable
(see Fig. 4.10), with an exponential trend
fixed by the polymer relaxation time, while the friction term in
the energy balance seems to be sub-dominant. Thus the mean square elongation
of polymers decay exponentially as
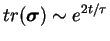 ,
with over-imposed strong oscillations which are anti-correlated to those of
the kinetic energy.
In this stage there is a continuous exchange of energy between the
velocity field and polymers and the decay of the two fields is
strongly coupled.
Since the trend of decay imposed by the polymers is steeper than
the exponential decay predicted by the friction, at a certain moment the
feedback term which slaves the kinetic energy decay
becomes smaller than friction one. From this point there is a
sharp decoupling of the dynamics of the two fields: the oscillations
disappear and each field decays exponentially with his own characteristic
time:
,
with over-imposed strong oscillations which are anti-correlated to those of
the kinetic energy.
In this stage there is a continuous exchange of energy between the
velocity field and polymers and the decay of the two fields is
strongly coupled.
Since the trend of decay imposed by the polymers is steeper than
the exponential decay predicted by the friction, at a certain moment the
feedback term which slaves the kinetic energy decay
becomes smaller than friction one. From this point there is a
sharp decoupling of the dynamics of the two fields: the oscillations
disappear and each field decays exponentially with his own characteristic
time: 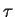 for polymers and
for polymers and
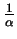 for velocity,
which in this late stage recovers the Newtonian behavior.
for velocity,
which in this late stage recovers the Newtonian behavior.




Next: Inverse energy cascade
Up: Active polymers
Previous: Lagrangian chaos reduction
Contents
Stefano Musacchio
2004-01-09
![]() where
where ![]() is the friction coefficient.
(see Fig. 4.10).
is the friction coefficient.
(see Fig. 4.10).
![\includegraphics[draft=false,scale=0.7]{P_decaypp.eps}](img679.png)