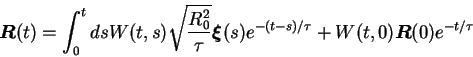 |
(3.11) |
The dumbbell model is able to reproduce the coil-stretch transition, which occurs when the stretching exerted by the flow overcomes the relaxation of polymer molecules.
The evolution of the polymer elongation can be obtained
following the trajectories of polymer molecules, and
Eq. (3.9) can be solved by characteristics as:
We are interested in the tail of the probability distribution function
of elongation ![]() for
for ![]() .
Following Balkovsky et al. [52],
at time large enough, when the initial condition is forgotten,
the events contributing to the right tail of the pdf are those
which have experienced large stretching.
The gradients of velocity field tends to orientate
the vector
.
Following Balkovsky et al. [52],
at time large enough, when the initial condition is forgotten,
the events contributing to the right tail of the pdf are those
which have experienced large stretching.
The gradients of velocity field tends to orientate
the vector
![]() in the direction of the
leading Lyapunov vector, and its length is determined
by the local value of the finite-time Lyapunov exponent
in the direction of the
leading Lyapunov vector, and its length is determined
by the local value of the finite-time Lyapunov exponent
![]() as
as
The convexity of the entropy function ensures that ![]() is positive if
is positive if
![]() .
In accordance with Eq. (3.15), the exponent
.
In accordance with Eq. (3.15), the exponent ![]() decreases when
decreases when ![]() increases, and it tends to zero as
increases, and it tends to zero as
![]() .
This means that when the value of the Weissenberg number
.
This means that when the value of the Weissenberg number
![]() exceeds unity the
the integral of the pdf diverges at large
exceeds unity the
the integral of the pdf diverges at large ![]() , and most of the
polymer molecule are stretched.
Below unity the pdf is stationary and only high moments of polymer
elongation diverge.
This is called ``coil-stretch'' transition.
, and most of the
polymer molecule are stretched.
Below unity the pdf is stationary and only high moments of polymer
elongation diverge.
This is called ``coil-stretch'' transition.
The exponent ![]() can be expressed via the equation
can be expressed via the equation
![]() , where
, where
![]() is the generalized Lyapunov exponent of order
is the generalized Lyapunov exponent of order ![]() .
Its value indicates the highest converging moment of
polymer elongation.
.
Its value indicates the highest converging moment of
polymer elongation.
In the coiled state, moments of polymer elongation
![]() with
with ![]() reach stationary values, while high moments with
reach stationary values, while high moments with
![]() diverge exponentially in time as:
diverge exponentially in time as:
In the Gaussian approximation of the
Cramér function ![]() , which holds near its minimum
, which holds near its minimum