Hyperbolic regions

In hyperbolic regions, where the predominant effect of velocity gradients is the stretching, using the incompressibility 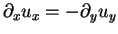$\partial_x u_x = - \partial_y u_y$ and defining

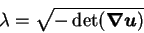$$\lambda = \sqrt{- \det ({\mbox{\boldmath$\nabla$}}{\mbox{\boldmath$u$}}) }$$ (A.12)

the matrix 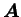${\mbox{\boldmath$A$}}$ can be diagonalized as

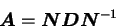$${\mbox{\boldmath$A$}} = {\mbox{\boldmath$N$}}{\mbox{\boldmath$D$}}{\mbox{\boldmath$N$}}^{-1}$$ (A.13)

where

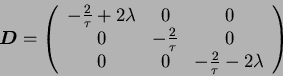$${\mbox{\boldmath$D$}} = \left( \begin{array}{ccc} -{2 \ove... ... 0 \\ 0 & 0 & -{2 \over \tau} - 2 \lambda \end{array}\right)$$ (A.14)

and the eigenvectors matrix 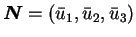${\mbox{\boldmath$N$}}= (\bar{u}_1,\bar{u}_2,\bar{u}_3 )$ is

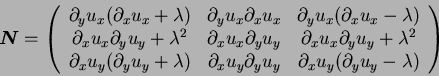$${\mbox{\boldmath$N$}} = \left( \begin{array}{ccc} \partial... ...rtial_x u_y (\partial_y u_y - \lambda) \\ \end{array}\right)$$ (A.15)

The exponential matrix is thus valued as

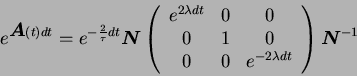$$e^{{\mbox{\boldmath$A$}}(t)dt} = e^{- {2 \over \tau} dt} {\... ...- 2 \lambda dt} \end{array}\right) {\mbox{\boldmath$N$}}^{-1}$$ (A.16)