



Next: Energy transfer
Up: Navier-Stokes equation
Previous: Reynolds number
Contents
The energy balance in absence of external forcing
for Navier-Stokes equation follows from
Eqs. (1.1,1.2).
The total kinetic energy of the fluid is
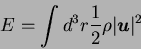 |
(1.9) |
and its temporal variation is
Assuming periodic boundary condition on a cubic volume of size 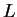
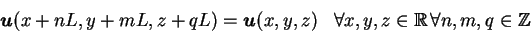 |
(1.11) |
or null boundary condition on a volume 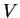
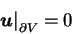 |
(1.12) |
the first two terms in the integral vanishes and using the identity
one gets
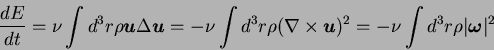 |
(1.14) |
where we have have introduced the vorticity of the fluid
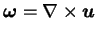 .
Defining the total enstrophy as
.
Defining the total enstrophy as
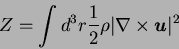 |
(1.15) |
the energy balance reads:
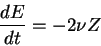 |
(1.16) |
which shows that in absence of external forcing and for 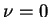 the kinetic energy is conserved by the dynamics, i.e.
it is an inviscid invariant. On the contrary in the limit
the kinetic energy is conserved by the dynamics, i.e.
it is an inviscid invariant. On the contrary in the limit 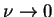 the energy dissipation rate does not vanish, but reaches
a constant value [7]:
the energy dissipation rate does not vanish, but reaches
a constant value [7]:
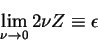 |
(1.17) |
This phenomenon is known as dissipative anomaly, and
implies that in the limit 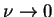 the total enstrophy must
grow as
the total enstrophy must
grow as
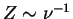 to compensate the decreasing viscosity.
The unbounded growth of enstrophy in three dimensions is the physical
origin of the dissipative anomaly, and it is possible because
of the vortex stretching, which produces
diverging velocity gradient in the limit
to compensate the decreasing viscosity.
The unbounded growth of enstrophy in three dimensions is the physical
origin of the dissipative anomaly, and it is possible because
of the vortex stretching, which produces
diverging velocity gradient in the limit 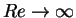 .
.




Next: Energy transfer
Up: Navier-Stokes equation
Previous: Reynolds number
Contents
Stefano Musacchio
2004-01-09