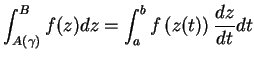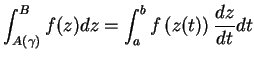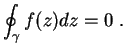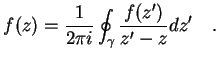

Next: Serie in campo complesso
Up: ab
Previous: Funzioni complesse di variabile
In questa unità vengono definiti gli
Integrali in campo complesso
e se ne dimostrano le principali proprietà.
Inizialmente (paragrafo 1.3.1) vengono brevemente richiamate
alcune nozioni sulle Curve nel piano complesso (l'argomento
è stato trattato nel corso di
???.
Viene quindi (paragrafo 1.3.2) definito l'integrale lungo una curva
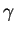 nel piano complesso (di equazione z = z(t),
con z(a) = A e z(b) = B) di una funzione complessa di variabile
complessa f(z):
nel piano complesso (di equazione z = z(t),
con z(a) = A e z(b) = B) di una funzione complessa di variabile
complessa f(z):
e dimostrato che esso soddisfa la Disuguaglianza di Darboux, ovvero che
è maggiorato in modulo dal prodotto della lunghezza della curva per il
massimo del valore che il modulo della funzione assume lungo la curva.
Successivamente viene dimostrato il fondamentale Teorema di Cauchy
(paragrafo 1.3.3): l'integrale di una funzione analitica lungo
una curva chiusa 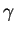 , tutta contenuta in un dominio semplicemente
connesso di analiticità per la funzione, è nullo:
, tutta contenuta in un dominio semplicemente
connesso di analiticità per la funzione, è nullo:
Due importanti conseguenze del Teorema di Cauchy sono il Corollario
al Teorema di Cauchy che afferma che l'integrale di una funzione analitica
tra i punti A e B non dipende dal particolare cammino di
integrazione
fintanto che i vari cammini sono deformabili uno nell'altro senza incontrare
singolarità,
ed il Teorema di Cauchy generalizzato che assicura che gli integrali
di una funzione analitica f(z) lungo due diverse curve chiuse
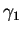 e
e 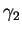 sono uguali se le due curve sono omotopicamente equivalenti
nel dominio di analiticità della funzione.
Infine viene dimostrata la validità della rappresentazione integrale di
Cauchy per una funzione analitica: data una funzione
f(z), analitica in un dominio semplicemente connesso,
ed una curva
sono uguali se le due curve sono omotopicamente equivalenti
nel dominio di analiticità della funzione.
Infine viene dimostrata la validità della rappresentazione integrale di
Cauchy per una funzione analitica: data una funzione
f(z), analitica in un dominio semplicemente connesso,
ed una curva 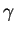 tutta contenuta in questo dominio, è possibile conoscere il valore della
funzione in tutti i punti interni alla curva una volta noti i valori che
essa assume su tutti i punti della curva:
tutta contenuta in questo dominio, è possibile conoscere il valore della
funzione in tutti i punti interni alla curva una volta noti i valori che
essa assume su tutti i punti della curva:
Al termine dello studio di questo capitolo sarai dunque in grado di:
- Valutare se l'integrale lungo una data curva chiusa di una funzione
analitica è banalmente nullo
Esercizi su..........
- Determinare se diversi integrali di cammino di una stessa funzione
analitica sono uguali o meno
Esercizi su..........
Alcuni link utili per l'approfondimento di questo argomento sono:


Next: Serie in campo complesso
Up: ab
Previous: Funzioni complesse di variabile
Marialuisa Frau
2003-05-30