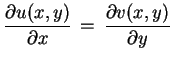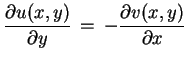

Next: Integrazione in campo complesso
Up: ab
Previous: Il campo complesso
In questa unità si introducono le
Funzioni complesse di variabile complessa,
che sono l'argomento fondamentale della prima parte del corso.
Inizialmente (paragrafo 1.2) viene definita una funzione
complessa di variabile complessa; dette x e y rispettivamente la
parte reale e la parte immaginaria della variabile complessa z, una
funzione complessa di variabile complessa f(z) si può scrivere come
e le due funzioni reali in 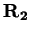 u(x,y) e v(x,y) sono dette
rispettivamente Parte Reale e Parte Immaginaria di f(z).
Viene quindi definito il concetto di
Funzione Derivabile (paragrafo 1.2.1)e dimostrato
che le Condizioni di Cauchy-Riemann (paragrafo 1.2.2)
u(x,y) e v(x,y) sono dette
rispettivamente Parte Reale e Parte Immaginaria di f(z).
Viene quindi definito il concetto di
Funzione Derivabile (paragrafo 1.2.1)e dimostrato
che le Condizioni di Cauchy-Riemann (paragrafo 1.2.2)
sono condizione necessaria e sufficiente perchè una
funzione sia derivabile.
Una funzione derivabile (ovvero che soddisfi le condizioni di Cauchy-Riemann)
in una regione aperta del piano complesso C è detta
Funzione Analitica.
Al termine dello studio di questo capitolo sarai dunque in grado di:
Alcuni link utili per l'approfondimento di questo argomento sono:


Next: Integrazione in campo complesso
Up: ab
Previous: Il campo complesso
Marialuisa Frau
2003-05-30