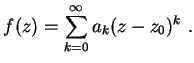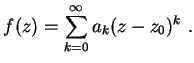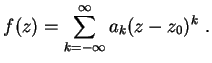

Next: Residui
Up: ab
Previous: Integrazione in campo complesso
In questa unità si tratta l'argomento delle
Serie di potenze in campo complesso
che sono lo strumento fondamentale per l'analisi delle proprietà
delle funzioni analitiche.
Inizialmente (paragrafo 1.4.1) vengono brevemente richiamate
le proprietà ed i criteri di convergenza delle serie di potenze in campo
complesso, che sono l'ovvia estensione di quelli validi per le serie di
potenze in campo reale (l'argomento è stato trattato nel corso di
???;
esercizi su questo argomento sono contenuti in
Esercizi sulle Serie in Campo Complesso.
Viene quindi illustrato (paragrafo 1.4.2)
uno dei risultati fondamentali di questo capitolo,
ovvero che una funzione f(z) analitica in un punto 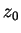 ammette sempre uno sviluppo in Serie di Taylor in un intorno
di
ammette sempre uno sviluppo in Serie di Taylor in un intorno
di 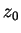 :
:
Tramite lo sviluppo in
Serie di Taylor si può facilmente definire quando il punto 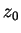 è uno
zero di ordine n per la funzione f(z) (paragrafo 1.4.3).
Successivamente viene definito il concetto di singolarità isolata
in un punto
è uno
zero di ordine n per la funzione f(z) (paragrafo 1.4.3).
Successivamente viene definito il concetto di singolarità isolata
in un punto 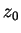 e si mostra come nell'intorno di una singolarità
isolata una funzione ammetta sempre uno sviluppo in
Serie di Laurent, ovvero uno sviluppo in serie di potenze di
e si mostra come nell'intorno di una singolarità
isolata una funzione ammetta sempre uno sviluppo in
Serie di Laurent, ovvero uno sviluppo in serie di potenze di 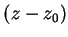 che comprende anche potenze negative (paragrafo 1.4.4):
che comprende anche potenze negative (paragrafo 1.4.4):
Lo sviluppo in Serie di Laurent viene poi usato (paragrafo 1.4.5)
per definire i due possibili tipi di singolarità isolate:
Poli di ordine n e Singolarità essenziali.
Al termine dello studio di questo capitolo sarai dunque in grado di:
Alcuni link utili per l'approfondimento sulle serie di potenze, ed in
particolare sulle serie di Taylor nel campo reale sono:
Link invece utili per l'approfondimento delle serie di potenze nel campo
complesso e delle serie di Laurent sono:


Next: Residui
Up: ab
Previous: Integrazione in campo complesso
Marialuisa Frau
2003-05-30